MAKE A MEME
View Large Image
| View Original: | Ratio test proof.svg (201x133) | |||
| Download: | Original | Medium | Small | Thumb |
| Courtesy of: | commons.wikimedia.org | More Like This | ||
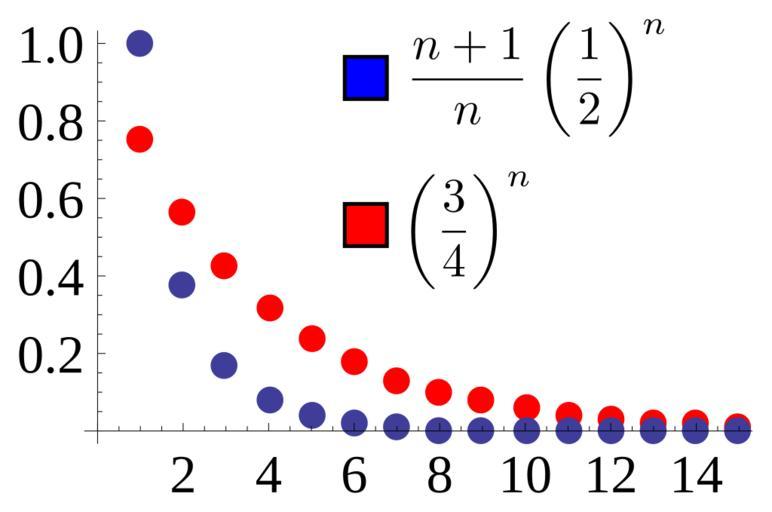
| Keywords: Ratio test proof.svg ratio test test is proven in the convergent case Given a sequence like the blue one for which the ratio of adjacent terms <math> a_ n+1 /a_n </math> converges to L < 1 we identify a ratio r L+1 /2 and show that for large enough n the sequence is dominated by the simple geometric sequence r<sup>k</sup> In this case the ratio of adjacent terms of the blue sequence converges to L 1/2 so we choose r 3/4 and r<sup>k</sup> dominates for all n �� 2 Source used to generate this chart is shown below own User Dcoetzee 2013-03-24 Cc-zero Source All source released under CC0 waiver Mathematica source to generate graph which was then saved as SVG from Mathematica <pre> Show 3/4 n n 1 15 PlotStyle -> Hue0 PointSizeLarge ListPlot n + 1 /n 1/2 n n 1 15 PlotStyle -> PointSizeLarge PlotRange -> All AxesStyle -> FontSize -> 14 </pre> LaTeX source for labels <pre> \left \frac 3 4 \right n \frac n+1 n \left \frac 1 2 \right n </pre> These were converted to SVG with http //www tlhiv org/ltxpreview/ and then the graph was embedded into the resulting document in Inkscape Axis fonts were also converted to Liberation Serif and the legend was added in Inkscape Sequence mathematics Convergence | ||||